Multiplier Design Verification

Description:

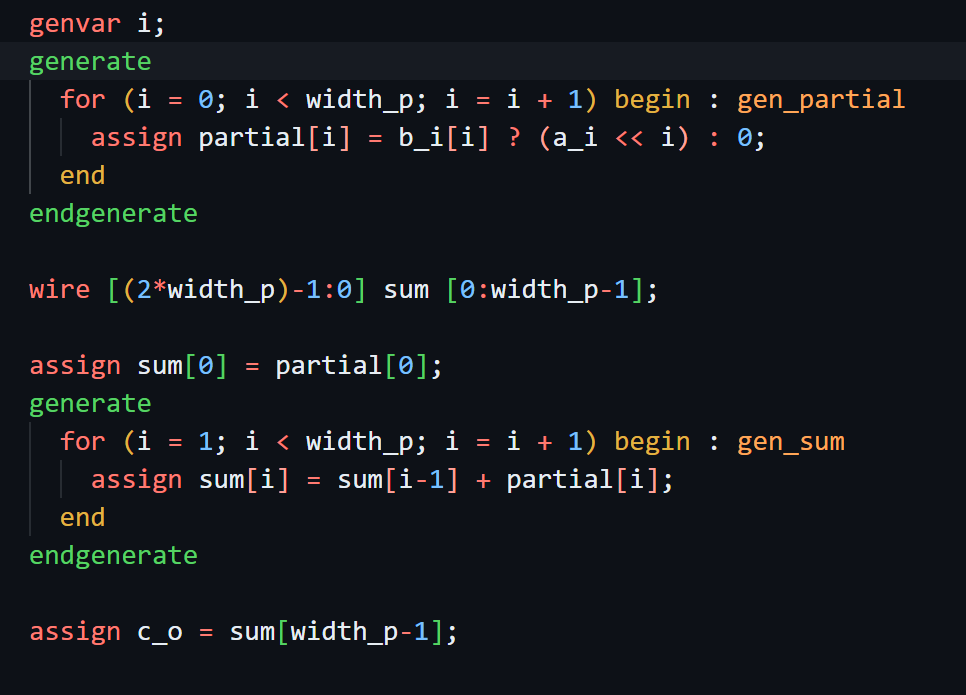
In this lab, I implemented a fully combinational 16-bit multiplier using the classic elementary binary multiplication algorithm, building the product from shifted partial sums rather than relying on the * operator or any optimized DSP blocks. My design generates a bank of partial products—one for each bit of the multiplier—by conditionally shifting the multiplicand based on whether each corresponding bit of b_i is set. This approach mirrors long multiplication in hardware, producing up to 16 aligned 32-bit intermediate values. I then built a structured adder cascade that accumulates these partial products sequentially, ensuring that each stage propagates a correct running sum into the next. The use of generate loops keeps the implementation scalable and clean while preserving synthesizability and readability.